Week1
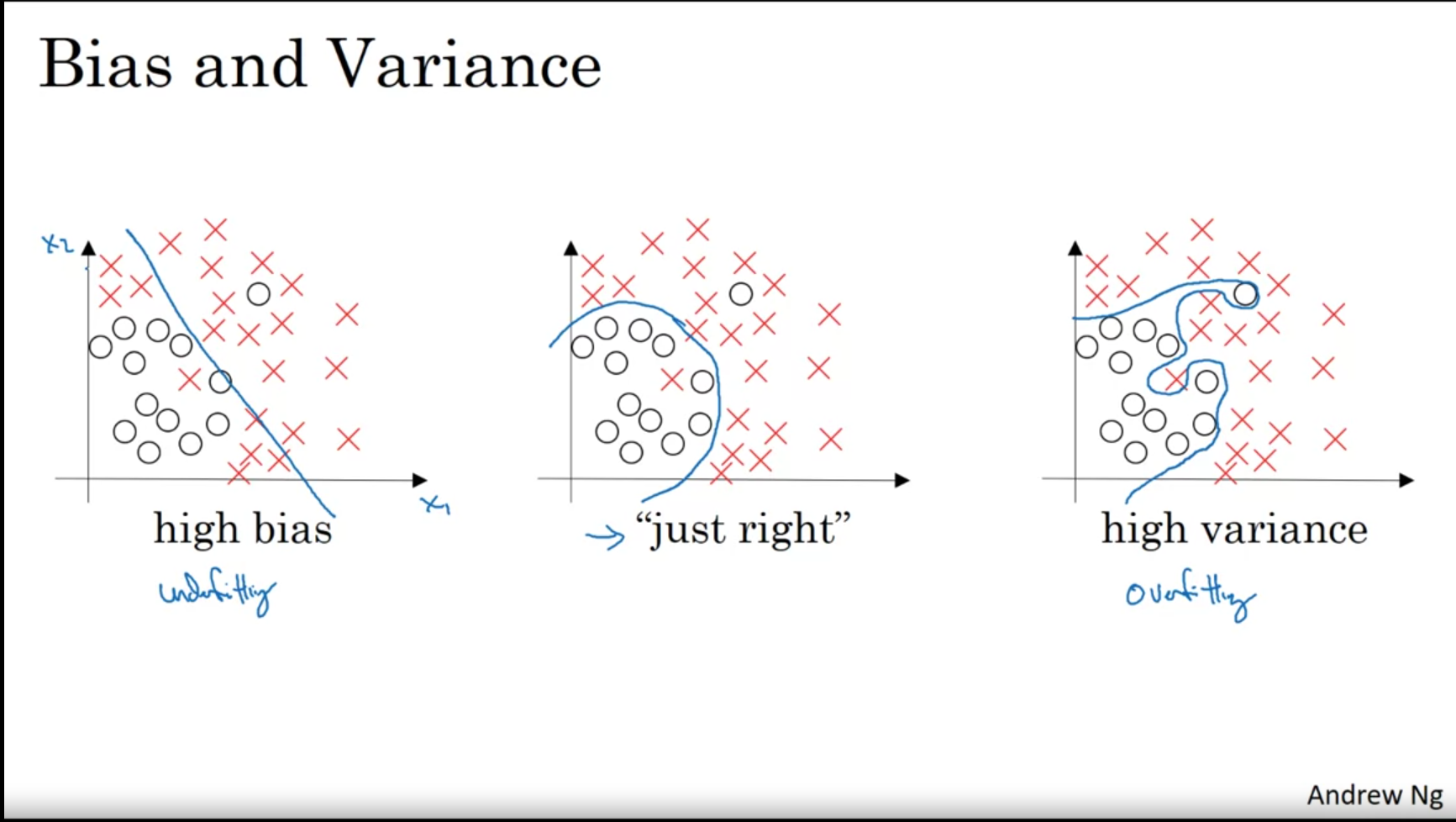
Bias and Variance
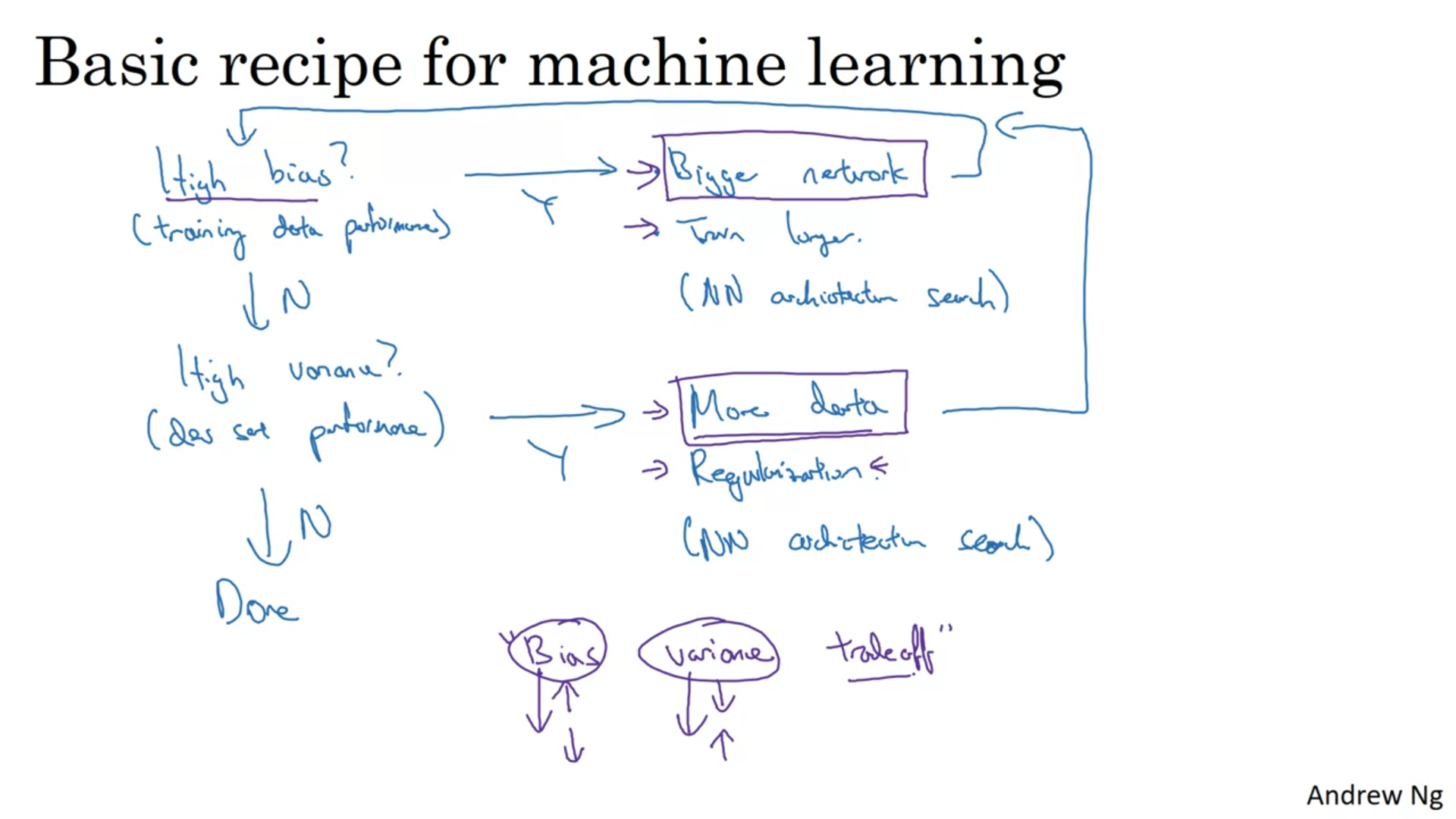
Regularization
variance → L2 and L1 Regularization
Frobenius Norm Weight decay
How regularization prevents overfitting?
How does regularization prevents overfitting lambdanın değerine göre (gerçekten büyük olması durumunda) w weight matrix i daha fazla 0 a yakın değerler içermeye başlıyor. Bu neural networkte bazı değrleri sıfırlıyor yani aynı layer sayısında ama her layerda daha az feature olan bir neural networkle karşılaşıyoruz. Daha simple bir neural networkü traşn ediyor gibi oluyoruz.
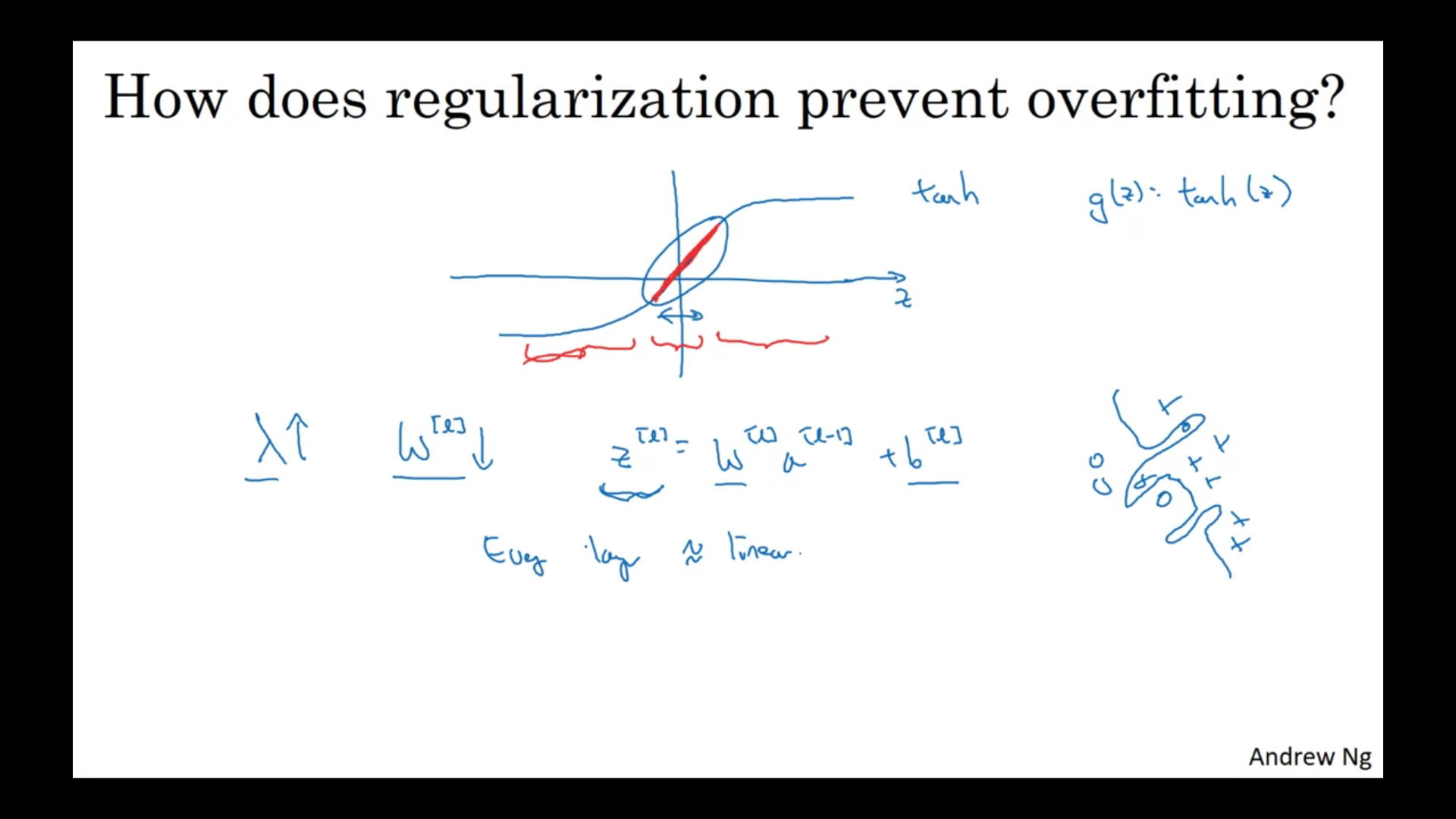
For example when activation function is tanh.
When lambda is big → W will be small → Z will be relatively small → small z values end up being nearly linear for tanh function → in the linear case overfitting will be prevented
Dropout
Dropout with some probability zeroing out some hidden layers while training → this way it makes us use a smaller network → regularization effect no dropout on the test time
Why dropout works?
With dropout inputs can be eliminated. yani o node a gelen inputlardan herhangi birine daha fazla odaklanmasını engelliyor ve weighti daha iyi dağıtabiliyor.
Farklı layerlarda farklı dropoutlar kullanılabilir. Daha az node u olan layerlarda droput kullanılmasa bile olur.
Augmentation
Early Stopping
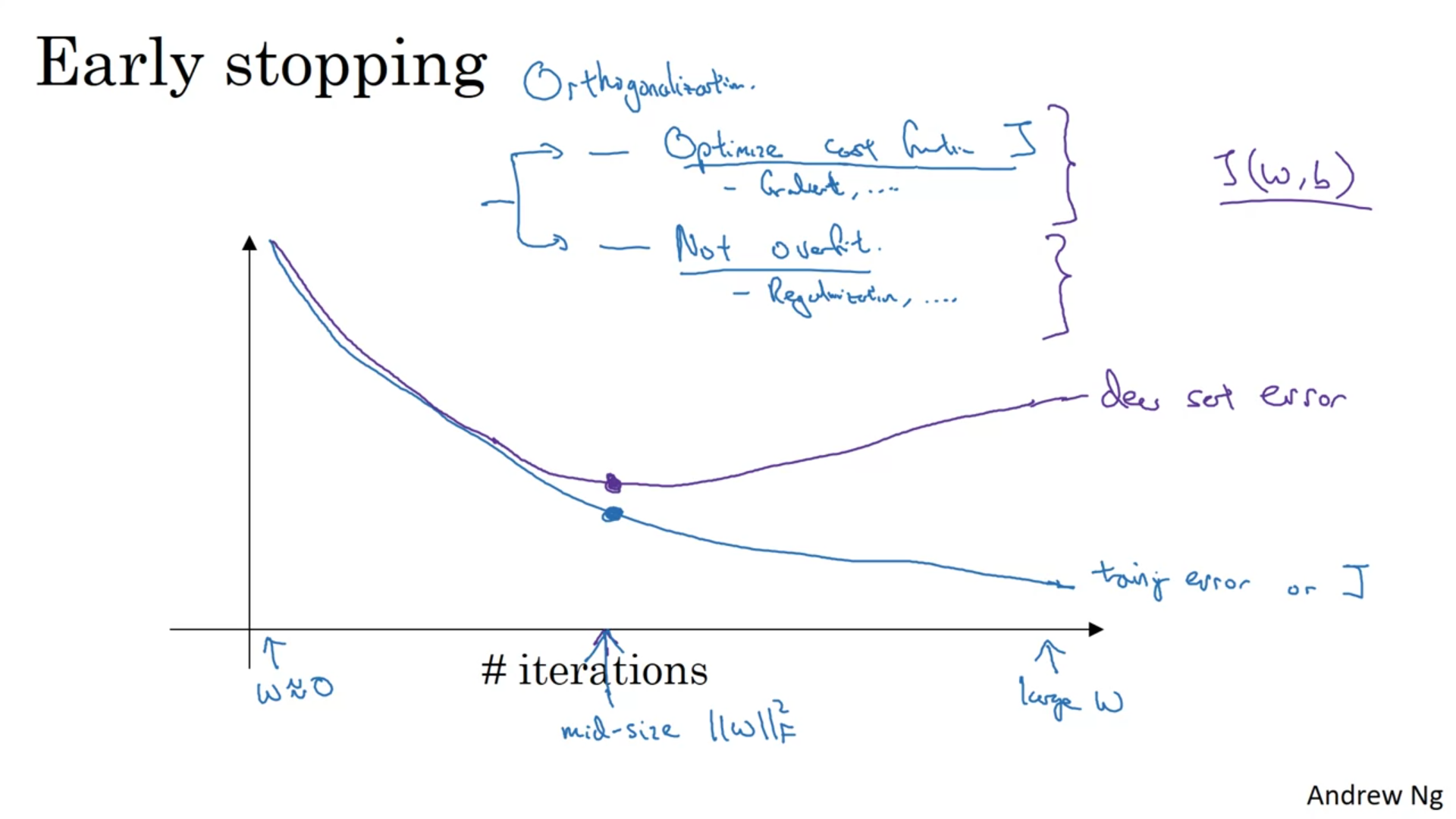
Instead of early stopping l2 regularization can be used but L2 is costly.
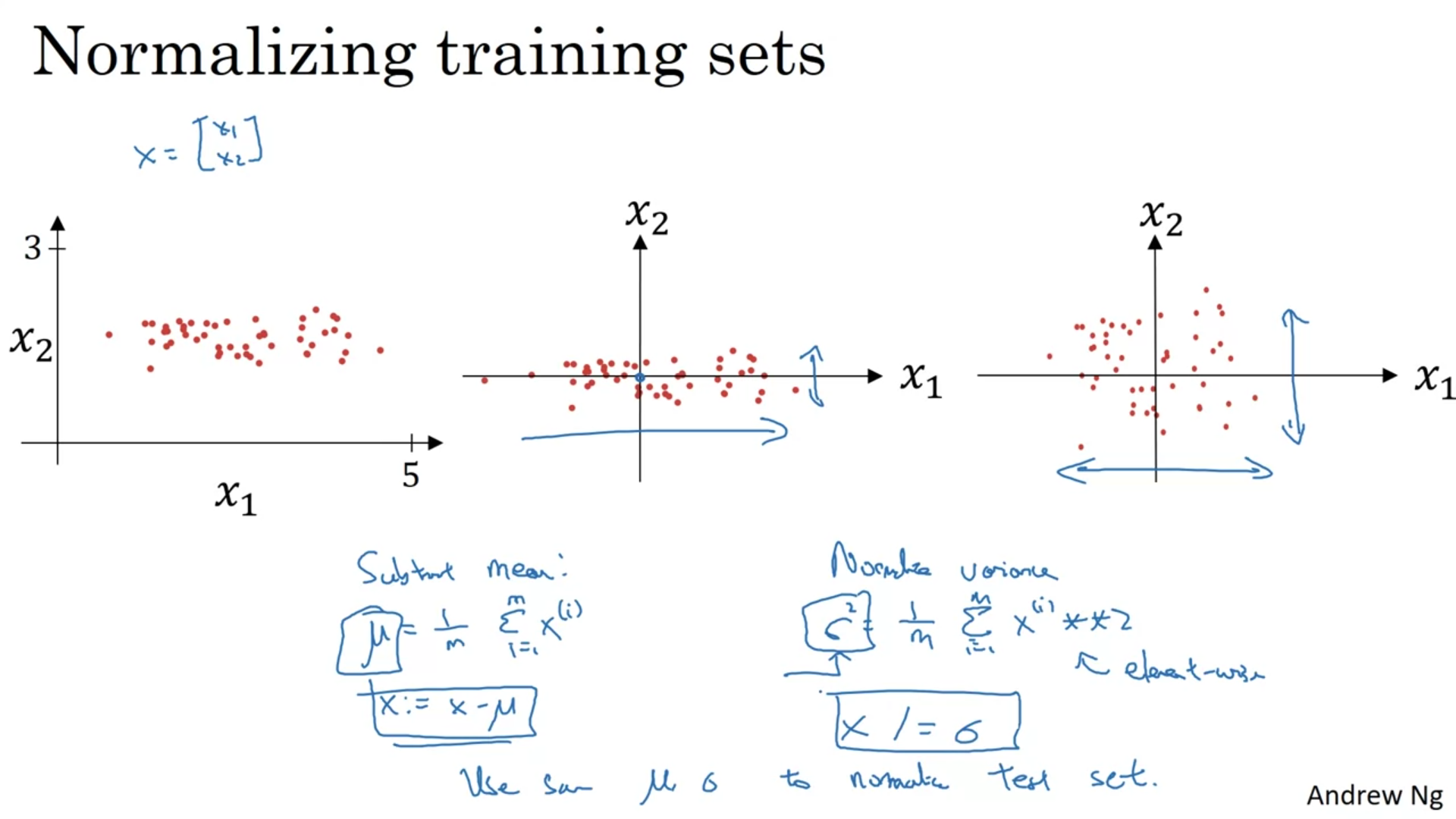
Normalization
Normalization is used to speed up the training Subtract mean → move the training set until it has zero mean Normalize variances → so that x and y will reside on the same intervals
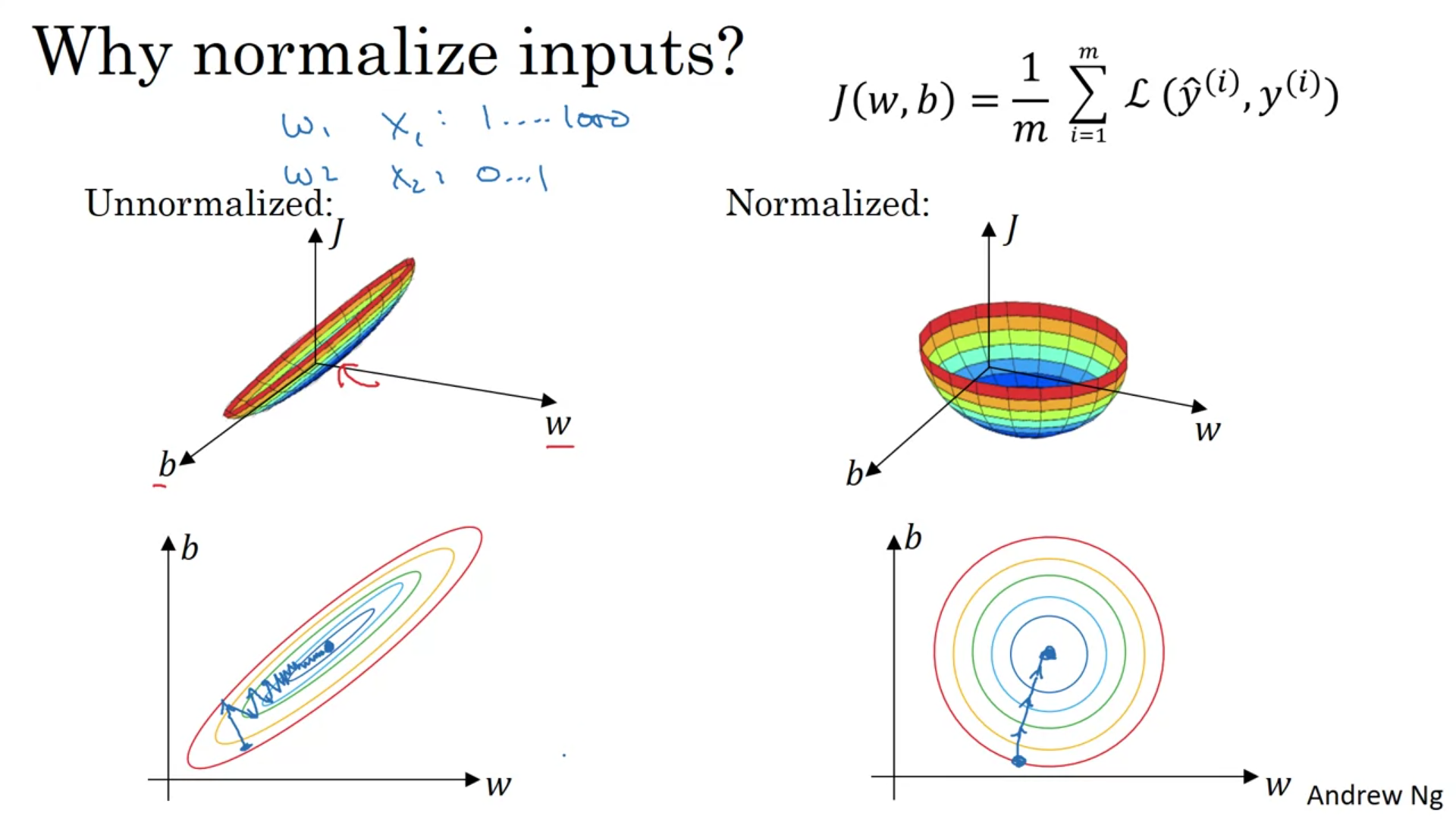
Why normalize inputs?
Normalized Loss function may results in faster gradient decrease with less steps to the minimum
Vanishing/Exploiding Gradient Problem
Özellikle deep neural networklerde daha da sıkıntılı bir problem
Solution: Better Weight Initialization
has input features. While randomly initializing weights, we normally multiply the values with 0.01. But instead multiplying with variance is better.
Farklı activation functionlar için farklı initialization stratejileri uygulanabilir. Bu aşağıdaki çözümler vanishing/exploiding gradient problemini çözüyor.
Week2: Optimization Algorithms
Daha hızlı train etmek ve daha hızlı sonuç almak adına optimization algoritmalarını kullanıyoruz.
Mini-batch
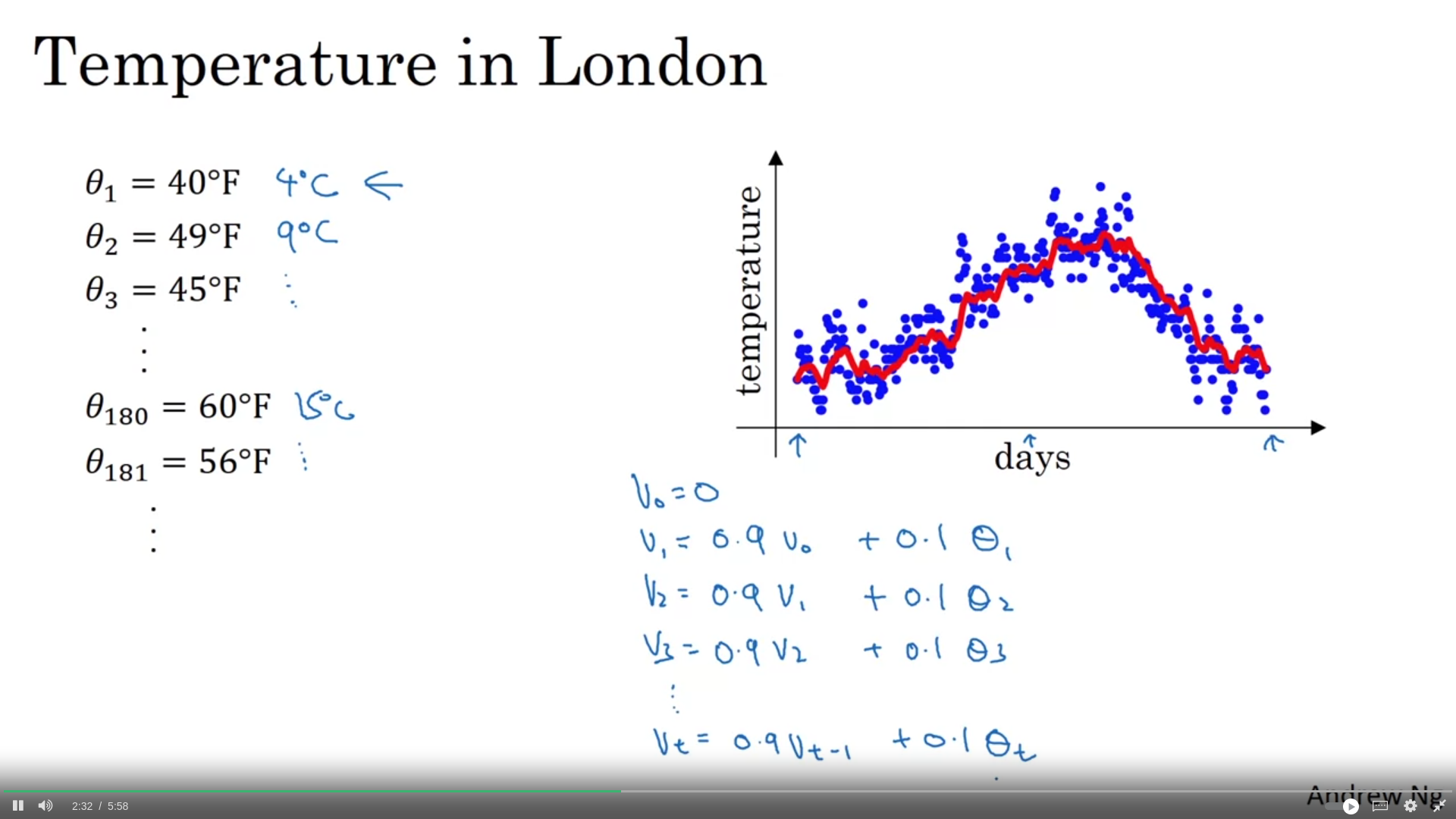
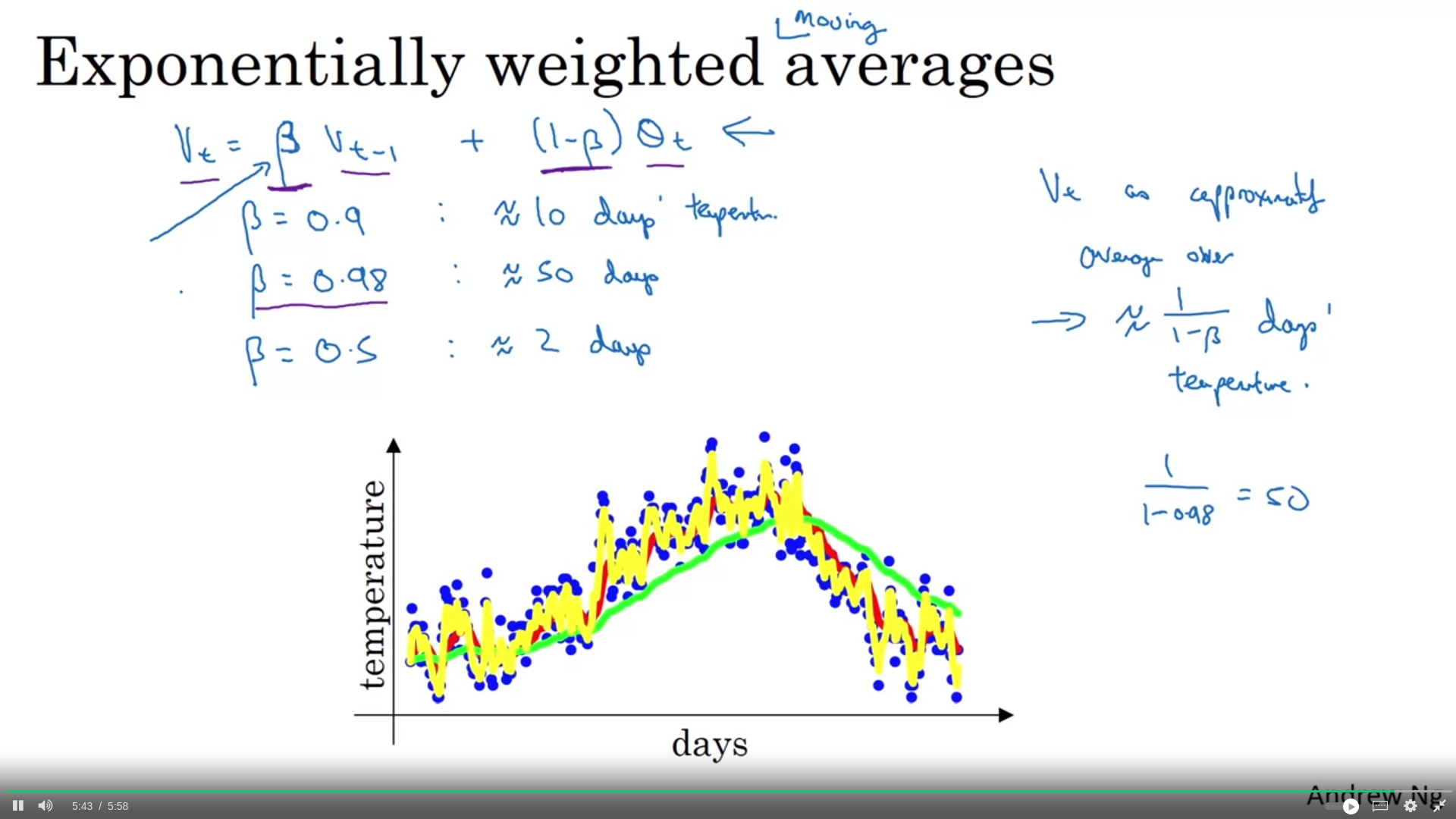
Depending on the , we average over days/units
V_0 = 0 introduces a bias that reduces the initial average values
Gradient Descent with momentum
Gradient descent update kısmında dw’yi farklı updateliyorsun.
soldaki kullanım tercih edilmeli
RMSProp
Gradient descent update ksımında dw ‘yi böleceğin bir değer hesaplıyorsun.
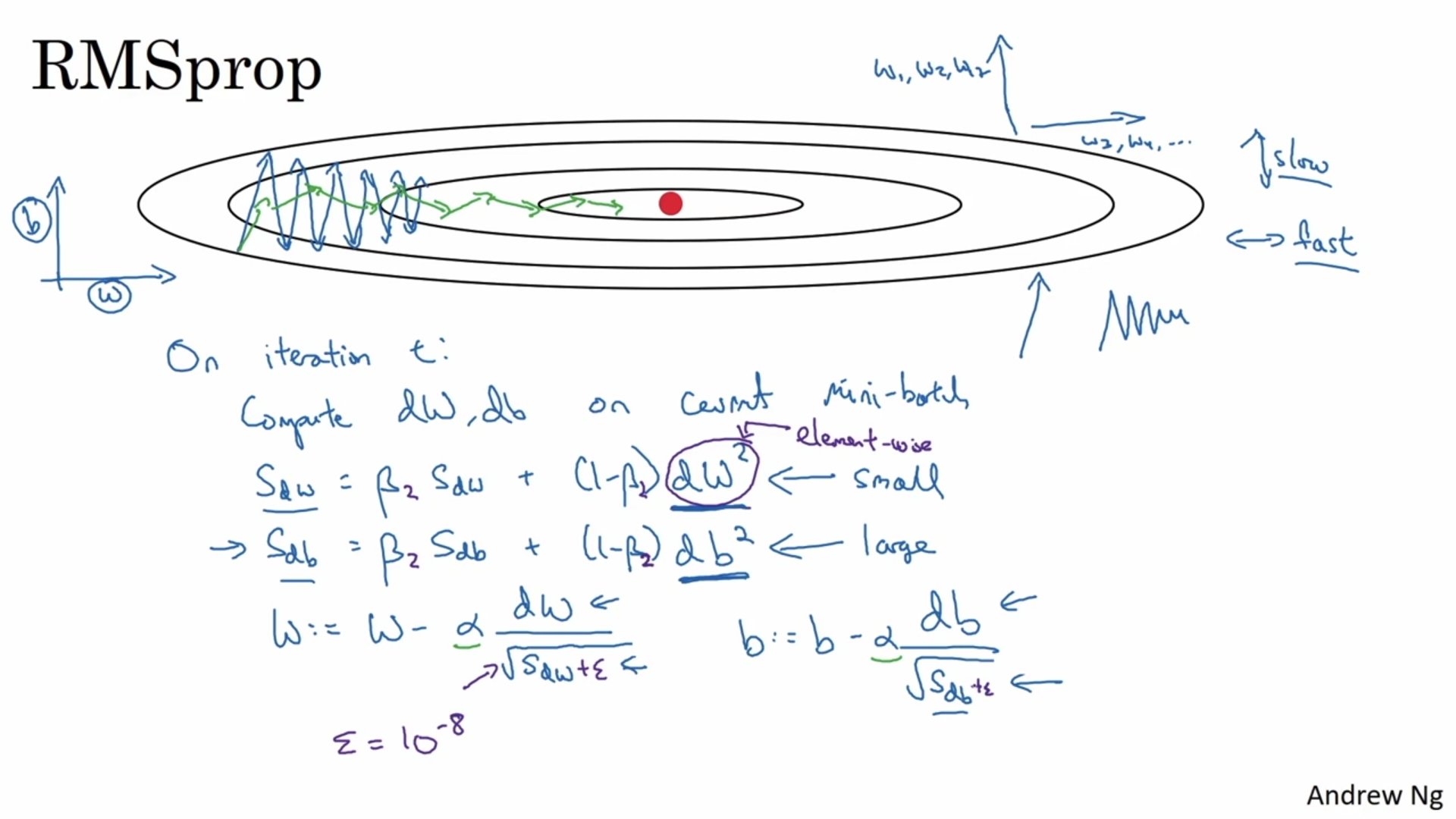
Adam (Adaptive moment estimation) optimizer
RMSProp + momentum = Adam
Learning Rate Decay
decay rate below becomes another hyperparameter
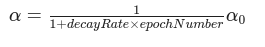slowly reduce alpha
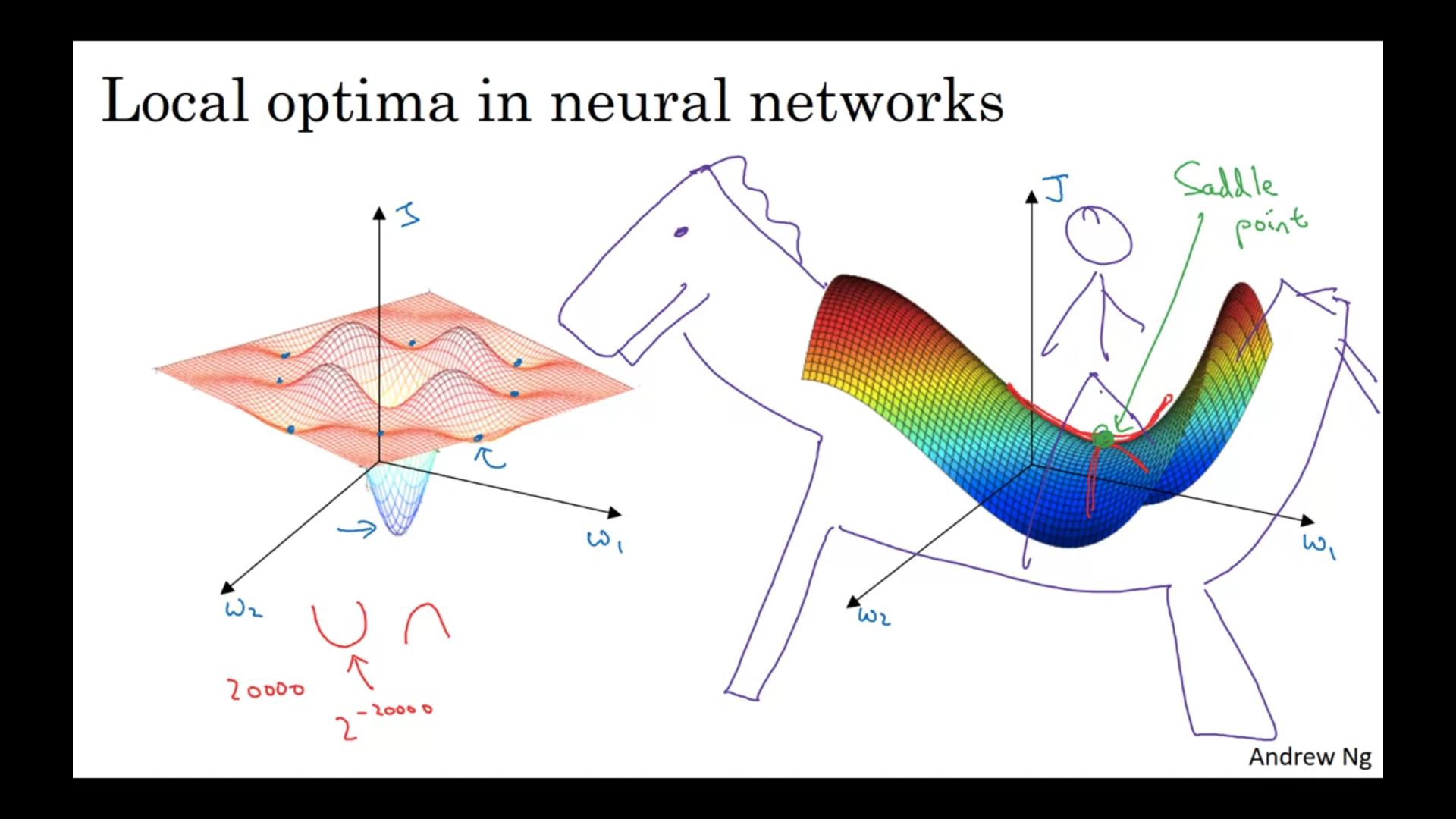
Local optima problem
When the derivative is close to 0 for a long time, it slow down the learning → plateaus most points of zero gradient in a cost function are saddle points, not local minimums
Week3: HyperParameter Tuning
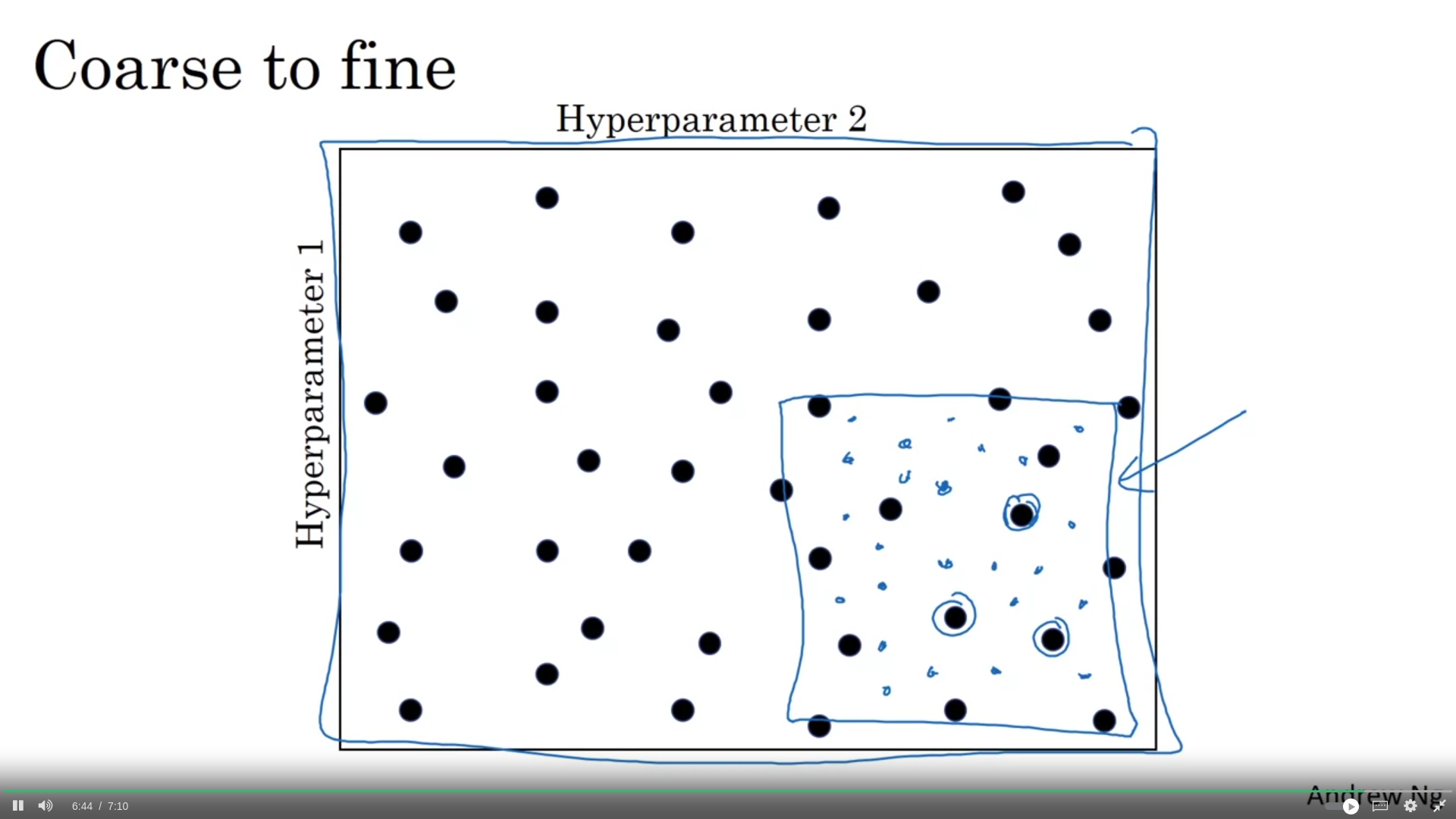
Büyük dikdörtgen içinde en iyi perform eden değerleri bulduktan sonra bu noktaları merkeze alarak daha küçük bir dörtgende daha sıkı bir arama yapılabilir.
Scaling while hyperparameter tuning
mesela learning rate için arama yaparken logaritmik scale’de uniform randomized bir search yapmak daha makul..
Yani scalingde r içinbir randomiation yapmalıyız.
Aynı şekilde burada da beta değerinin 0.9 olması ile 0.999 olması arasında çok fark var. 0.9 olması son 10 günlük averagea bakılıyor olması anlamına gelirken 0.999 olması son 1000 günlük average a bakılıyor olmasına denk. Bu durumda 1 - beta üzerinden logaritmik bir randomization uygulanmalı.
Week3: Batch normalization
eğer sadece z_norm kullanacak olsak hidden unitler için tüm değerler mean 0 ve variance 1 olacaktı. ama belki onlar için farklı bir distribution olması daha anlamlı olabilri. O yüzden z_norm’u iki parametre ile linearization yaparak z_tilda hesaplıyoruz.
normalizing z (before activation) is much more preferred to normalizing a (after activation)
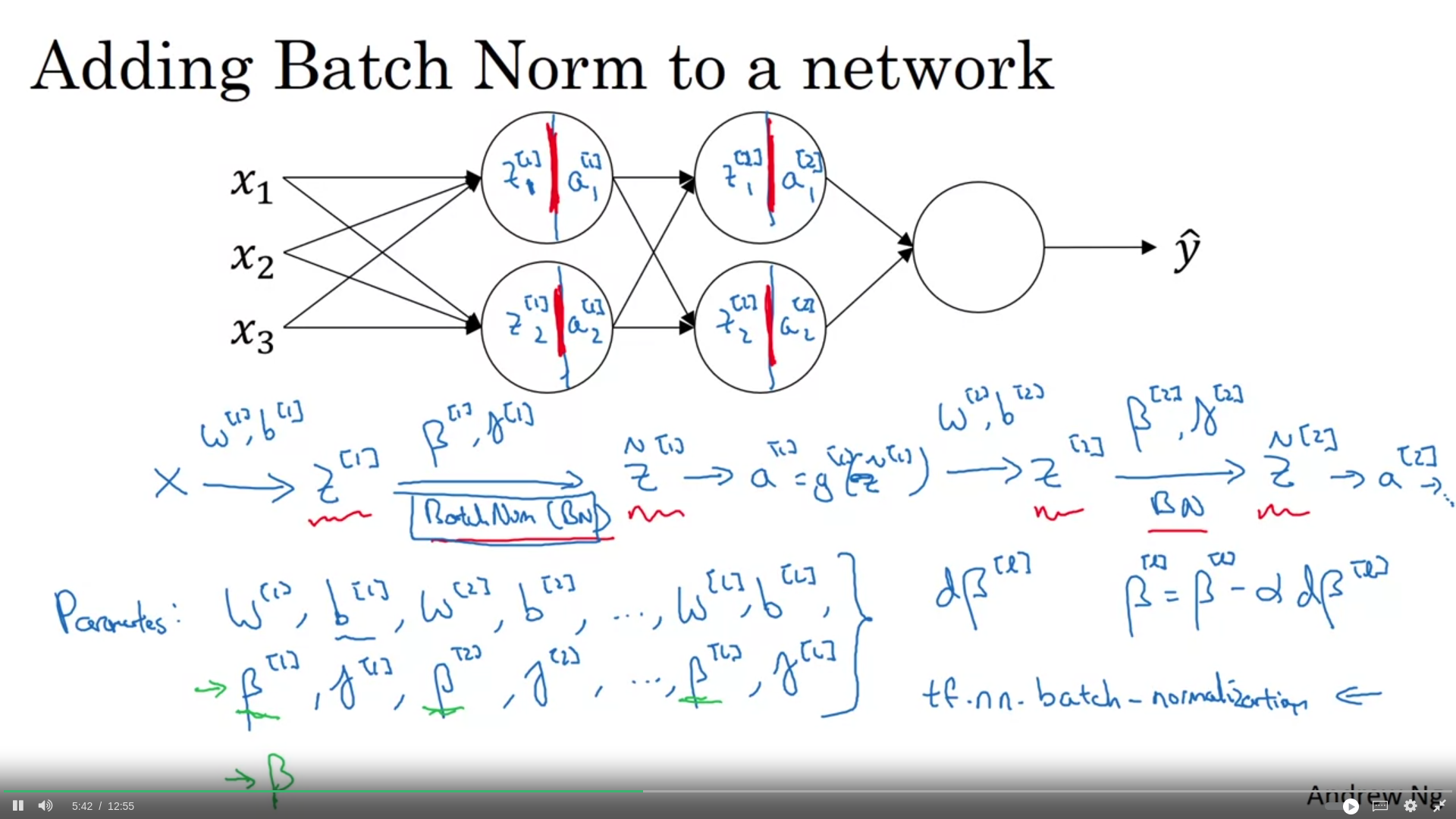
Because batch norm zeroes out the mean, if we use batch norm for hidden units, we dont need to learn b parameter. Instead beta parameter is enough
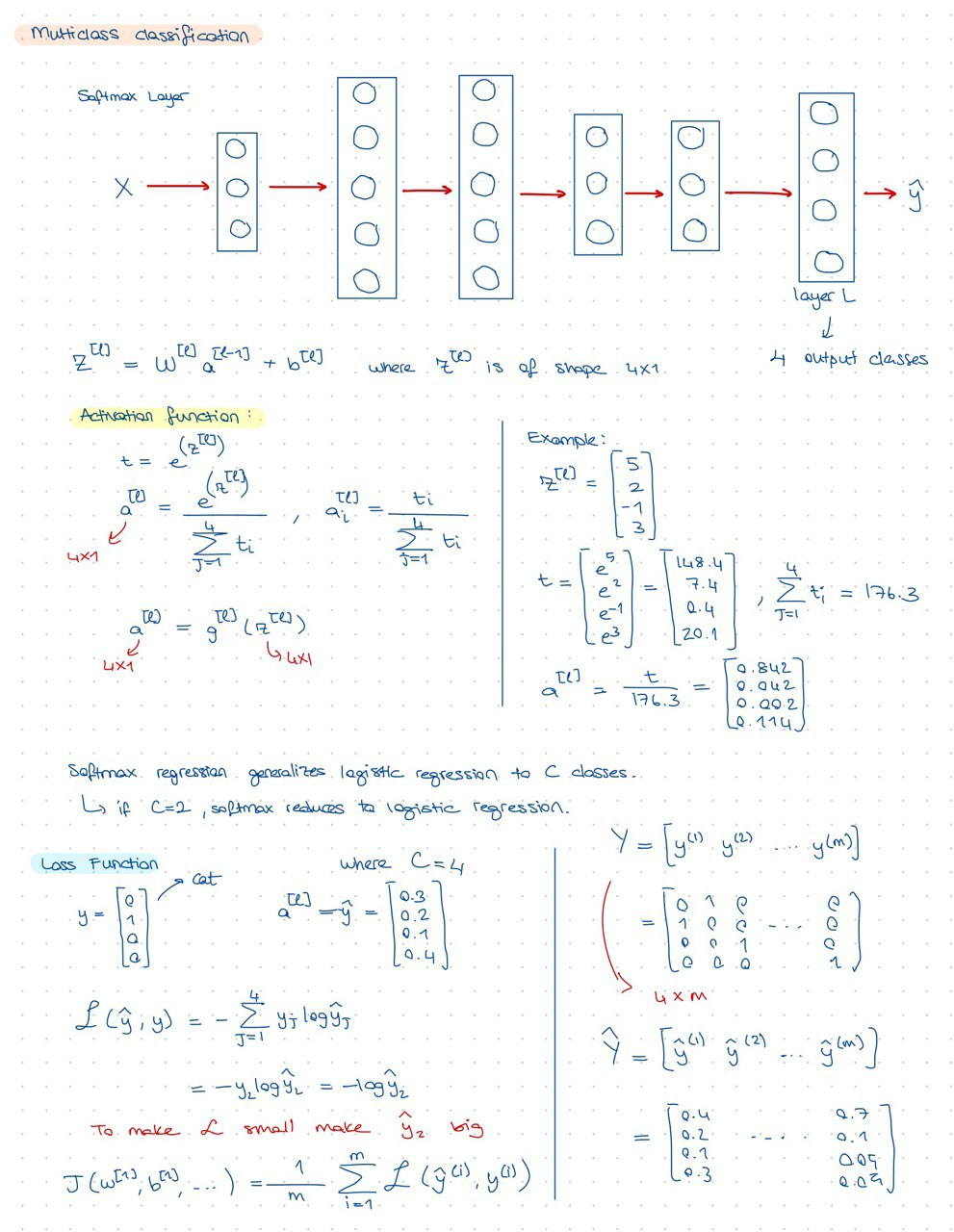
Week3: multiclass classification
